如何通俗地解释泰勒公式?
185 个回答
泰勒公式一句话描述:就是用多项式函数去逼近光滑函数。
先来感受一下:

此处有互动内容,需要流量较大,最好有wifi处打开,土豪请随意。
点击此处前往操作。
设 n 是一个正整数。如果定义在一个包含 a 的区间上的函数 f 在 a 点处 n+1 次可导,那么对于这个区间上的任意 x 都有: \displaystyle f(x)=\sum _{n=0}^{N}\frac{f^{(n)}(a)}{n!}(x-a)^ n+R_ n(x) ,其中的多项式称为函数在 a 处的泰勒展开式, R_ n(x) 是泰勒公式的余项且是 (x-a)^ n 的高阶无穷小。----维基百科
泰勒公式的定义看起来气势磅礴,高端大气。如果 a=0 的话,就是麦克劳伦公式,即\displaystyle f(x)=\sum _{n=0}^{N}\frac{f^{(n)}(0)}{n!}x^ n+R_ n(x) ,这个看起来简单一点,我们下面只讨论麦克劳伦公式,可以认为和泰勒公式等价。
1.多项式的函数图像特点
\sum _{n=0}^{N}\frac{f^{(n)}(0)}{n!}x^ n 展开来就是 f(0)+f'(0)x+\frac{f''(0)}{2!}x^2+\cdots +\frac{f^{(n)}(0)}{n!}x^ n , f(0) , \frac{f''(0)}{2!} 这些都是常数,我们暂时不管,先看看其中最基础的组成部分,幂函数有什么特点。


可以看到,幂函数其实只有两种形态,一种是关于 Y 轴对称,一种是关于原点对称,并且指数越大,增长速度越大。
那幂函数组成的多项式函数有什么特点呢?

怎么才能让 x^2 和 x^9 的图像特性能结合起来呢?

我们来动手试试看看系数之间如何压制的:

此处有互动内容,需要流量较大,最好有wifi处打开,土豪请随意。
点击此处前往操作。
通过改变系数,多项式可以像铁丝一样弯成任意的函数曲线。送你一颗心(虽然是隐函数,意思一下):

2.用多项式对 e^ x 进行逼近
e^ x 是麦克劳伦展开形式上最简单的函数,有 e 就是这么任性。
e^ x=1+x+\frac{1}{2!}x^2+\cdots + \frac{1}{n!}x^ n + R_ n(x)

增加一个 \frac{1}{4!}x^4 看看。

增加一个 \frac{1}{5!}x^5 看看。

可以看出, \frac{1}{n!}x^ n 不断的弯曲着那根多项式形成的铁丝去逼近 e^ x 。并且 n 越大,起作用的区域距离0越远。
3.用多项式对 sin(x) 进行逼近
sin(x) 是周期函数,有非常多的弯曲,难以想象可以用多项式进行逼近。
sin(x)=x-\frac{1}{3!}x^3+\cdots +\frac{(-1)^ n}{(2n+1)!}x^{(2n+1)}+ R_ n(x) 。

同样的,我们再增加一个 \frac{1}{7!}x^7 试试。

可以看到 \frac{1}{7!}x^7 在适当的位置,改变了 x-\frac{1}{3!}x^3+\frac{1}{5!}x^5 的弯曲方向,最终让x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\frac{1}{7!}x^7 更好的逼近了 sin(x) 。
一图胜前言,动手看看 sin(x) 的展开吧:

此处有互动内容,需要流量较大,最好有wifi处打开,土豪请随意。
点击此处前往操作。
4.泰勒公式与拉格朗日中值定理的关系
拉格朗日中值定理:如果函数 f(x) 满足,在 [a,b] 上连续,在 (a,b) 上可导,那么至少有一点 \theta ( a<\theta <b )使等式 f'(\theta )=\frac{f(a)-f(b)}{a-b} 成立。----维基百科
数学定义的文字描述总是非常严格、拗口,我们来看下拉格朗日中值定理的几何意义:

这个和泰勒公式有什么关系?泰勒公式有个余项 R_ n(x) 我们一直没有提。
余项即使用泰勒公式估算的误差,即 \displaystyle f(x)-\sum _{n=0}^{N}\frac{f^{(n)}(a)}{n!}(x-a)^ n=R_ n(x)
余项的代数式是, R_ n(x)=\frac{f^{(n+1)}(\theta )}{(n+1)!}(x-a)^{(n+1)} ,其中 a<\theta <x 。是不是看着有点像了?
当 N=0 的时候,根据泰勒公式有, f(x)=f(a)+f'(\theta )(x-a) ,把拉格朗日中值定理中的 b 换成 x ,那么拉格朗日中值定理根本就是 N=0 时的泰勒公式。
结合拉格朗日中值定理,我们来看看 N=0 的时候,泰勒公式的几何意义:

当 N=0 的时候,泰勒公式几何意义很好理解,那么 N=1,2,\cdots 呢?
这个问题我是这么理解的:首先让我们去想象高阶导数的几何意义,一阶是斜率,二阶是曲率,三阶四阶已经没有明显的几何意义了,或许,高阶导数的几何意义不是在三维空间里面呈现的,穿过更高维的时空才能俯视它的含义。现在的我们只是通过代数证明,发现了高维投射到我们平面上的秘密。
还可以这么来思考泰勒公式,泰勒公式让我们可以通过一个点来窥视整个函数的发展,为什么呢?因为点的发展趋势蕴含在导数之中,而导数的发展趋势蕴含在二阶导数之中......四不四很有道理啊?
5.泰勒公式是怎么推导的?
很多同学看到这段时,可能有点看不懂,我在牛顿插值的几何解释是怎么样的? - 知乎,这个回答里尝试重新作答了。
根据“以直代曲、化整为零”的数学思想,产生了泰勒公式。

如上图,把曲线等分为 n 份,分别为 a_1 , a_2 , \cdots , a_ n ,令 a_1=a , a_2=a+\Delta x, \cdots , a_ n=a+(n-1)\Delta x 。我们可以推出( \Delta ^2 , \Delta ^3 可以认为是二阶、三阶微分,其准确的数学用语是差分,和微分相比,一个是有限量,一个是极限量):
f(a_2)=f(a+\Delta x)=f(a)+\Delta f(x) f(a_3)=f(a+2\Delta x)=f(a+\Delta x)+\Delta f(a+\Delta x)=f(a)+2\Delta f(x)+\Delta ^2f(x) f(a_4)=f(a+3\Delta x)=f(a)+4\Delta f(x)+6\Delta ^2f(x)+4\Delta ^3f(x)+\Delta ^4f(x)
也就是说,f(x)全部可以由 a 和 \Delta x 决定,这个就是泰勒公式提出的基本思想。据此的思想,加上极限 \Delta x \to 0 ,就可以推出泰勒公式。
6.泰勒公式的用处
多项式这种函数是我们可以亲近的函数,它们很开放、很坦白,心里想什么就说什么,比如 f(x)=2-3x ,这个多项式会告诉我们想问的任何消息,甚至更多,譬如,我们问:“嘿,老兄,你在4那点的值是多少?”这时 f(x) 会毫不犹豫的回答:“你把4代进来,就会得到 2-3\times 4=-10 ,顺便告诉你,我最近长了奇怪的疹子,痒的要命,还好这两天症状减轻了...”。但是 ln(x) 阴暗、多疑,要是问它:“嗨,你在3的值是多少啊?”你得到的答案可能是:“你要干什么?为什么打听别人的私事?你以为凭着你那点加减乘除的三脚猫功夫就可以查出我的底细?况且我在3的值是多少,干你什么事!”----《微积分之倚天宝剑》
泰勒公式最直接的一个应用就是用于计算,计算机一般都是把 sin(x) 进行泰勒展开进行计算的。
泰勒公式还可以把问题简化,比如计算, \displaystyle \lim _{x \to 0}\frac{sin(x)}{x} ,代入 sin(x) 的泰勒展开有:\displaystyle \lim _{x \to 0}\frac{sin(x)}{x}=\lim _{x \to 0}\frac{x+o(x^3)}{x}=1 ,其中 o(x^3) 是泰勒公式里面的余项,是高阶无穷小,\displaystyle \lim _{x \to 0}o(x^3)=0 。解题神器有没有?
文章最新版本在(有可能会有后续更新):如何通俗地解释泰勒公式?
更多内容推荐马同学图解数学系列
这里主要是对高票答案的总结, 外加一些自己的理解, 希望能写的更通俗易懂一些, 方便大家理解.
- 麦克劳林公式
对于一些复杂的函数, 要研究其性质往往是比较困难的. 而多项式函数的性质往往比较简单, 所以有时候, 为了方便研究, 我们可能会想着: 能不能用一个多项式函数去近似一个复杂的函数?
比如说, 现在我们想在点0附近, 用一个多项式函数, 去近似一个复杂函数 y = e^x , 那我们应该怎么做呢?
我们知道当x=0时, e^x = 1, 所以不妨拿一个"当x=0时, y值也为1的函数"来近似试试, 比如说: y = 1

可以看到, 在x=0这一点上, 两个函数的值都是1, 但在x=0的邻域, 这两个函数的图像一点都不相似, 所以这个近似效果一般...
那如何让近似效果更好一些呢, 可以想到, 不妨用导数试试. 导数可以反应函数在某一点的变化率, 如果两个函数在x=0处, 除了y值相同, 变化率也相同, 那两个函数应该会更相似一些.
(e^x)' = e^x , 当x=0时, e^x 的导数为1
所以我们需要近似函数在x=0处的导数也为1, 比如说这个函数: y = 1 + x, 其导数y'等于常数1, 在x=0处的导数自然也为1
现在: 原始函数 e^x, 近似函数y = 1 + x, 这两个函数在x=0处, 除了y值相同, 导数也相同. 我们来看看这两个函数的图像

两个函数的图像更接近了, 看来这个思路是正确的, 那沿着这个思路, 如果让近似函数在x=0处的二阶导, 和e^x在x=0处的二阶导也相同呢...即在x=0处, 两个函数变化率的变化率也相同...
(e^x)'' = e^x
所以 e^x 在x=0处的二阶导也为1
那么我们选定近似函数: y = 1 + x+x^2/2
近似函数在x=0时, y=1,
近似函数的一阶导为1+x, 当x=0时, 一阶导为1,
近似函数的二阶导为常数1, 当x=0时, 二阶导也为1,
这些值和 e^x 在x=0处的y值, 一阶导, 二阶导的值是相同的, 来看看两个函数的图像

更相近了...
然后我们按照这个思路, 来试试三阶导
让近似函数在x=0处的y值, 一阶导, 二阶导, 三阶导的值 = e^x 在x=0处的y值, 一阶导, 二阶导, 三阶导的值
比如近似函数为: y =1+x+x^2/2+x^3/6 (这个函数是满足上述条件的, 这里就不验证了)
看一下图像:

更相近了..
再来看几张:



按这个思想, 假设原始函数在x = 0处n阶可导(比如 e^x在x=0处就是n阶可导)
如果让近似函数在x=0处的y值, 一阶导, 二阶导 ...n阶导的值 = e^x 在x=0处的y值, 一阶导, 二阶导 ...n阶导的值. 则可以推测此时两个函数的图像应该会很相似, 或者说近似函数对原始函数的近似效果应该会很好, 事实也确实如此.
麦克劳林公式(麦克劳林公式就是x0=0时的泰勒公式, 后面会具体讲泰勒公式)就是在描述: 如何找到满足上述条件的近似多项式函数, 写成公式大概是:

左侧是原始函数, 右侧是近似多项式函数
而两者之间的关系只是约等于, 或者说是近似. 实际上, 完整的麦克劳林公式是这样的:

后面的 ○(x^n) 是佩亚诺余项, 加上这个佩亚诺余项, 左右就相等了
麦克劳林公式的含义就是: 如何在x=0附近, 用一个多项式函数(等号右侧的函数), 去近似一个复杂函数(等号左侧的函数)
(这里稍微说一下佩亚诺余项: 在麦克劳林公式中, 佩亚诺余项 ○(x^n) 是个当x→0时比x^n高阶的无穷小, 这也就说明, 在x=0附近, 用麦克劳林公式产生的多项式函数(不含余项部分)去近似原始函数时, x离0越近的地方, 近似的误差越小, 近似效果越好, x离0越远的地方, 近似的误差越大, 近似效果越坏)
2. 为什么麦克劳林公式会是这种形式
麦克劳林公式:

为什么等号右侧的多项式(不含最后的余项)要写成这种形式呢? 其实理论上, 右侧的多项式也可以写成别的形式, 其本质只是为了满足下面这个条件:
让右侧多项式函数在x=0处的y值, 一阶导, 二阶导 ...n阶导的值 = 被近似函数在x=0处的y值, 一阶导, 二阶导 ...n阶导
这里的多项式
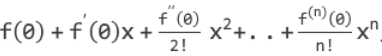
只是满足这个条件的一种形式. 如果还有别的形式的函数可以满足这个条件, 它也可以替换掉麦克劳林公式中的的多项式部分.
这里引用下"各向异性角点解"同学的一段话:
泰勒展开(或者说麦克劳林公式)并不是唯一的,因为任何在对应阶求导后能够消失并只留下导数值的函数,都可以作为泰勒展开的备胎。可惜的是,幂函数与阶乘的组合,是我们已知的唯一具有上述性质的函数,因此,这种唯一性决定了泰勒展开能够且仅能够由幂函数表示。
3. 泰勒公式

麦克劳林公式只是泰勒公式在x0=0时的特殊情况, 现在抛开x0=0, 让x0可以是函数定义域中的任意值(只要在x0处n阶可导就行), 就变成了泰勒公式
理解了麦克劳林公式, 很快就能理解泰勒公式了: 泰勒公式用于在x0附近, 用一个多项式函数(等号右侧的函数), 去近似一个复杂函数(等号左侧的函数)
4. 总结
I. 泰勒公式的作用是描述如何在x0点附近, 用一个多项式函数去近似一个复杂函数.
II. 之所以能实现这种近似, 背后的逻辑是:
让近似多项式函数在x=x0处的y值, 一阶导, 二阶导 ...n阶导的值 = 原始函数在x=x0处的y值, 一阶导, 二阶导 ...n阶导
即, 如果函数A和函数B在某一点的值一样, 变化率一样, 变化率的变化率一样, 变化率的变化率的变化率也一样...
就这样层层深入, 无论深入到哪一个维度, 关于这一点的变化率, 函数A和函数B都是一样的, 那就可以推断:
在这一点上, 函数A和B应该是一样的
在这一点附近, 函数A和B应该很相似
离这一点越远, 函数A和B的相似程度就越难以保证
...
---
最后需要说明的是, 这篇答案更多的是: 在默认泰勒公式正确性的前提下, 告诉大家如何去"直观感受"这种正确性, 去理解这么长的一串公式背后所表达的简单含义, 并粗略地理解公式成立的大体原因. 至于泰勒公式究竟是如何推导出来的, 其背后经过了怎样地严格证明, 这里并没有真正提及, 这些内容需要大家去查阅更多的资料, 进行深入的理解...

